1. Доказательство от обратного (противного).
Один из часто используемых методах в доказательстве. Его принцип состоит в том, что доказательство суждения (тезиса) осуществляется через опровержение противоречящего ему суждения (антитезиса). Опровержение антитезиса достигается установлением факта того, что он не совместим с каким-то уже заведомо истинным суждением.
Доказательство истинности утверждения A проводится следующим образом. Сначала принимают, что суждение A - ложно. Затем доказывают, что в таком случае, некоторое утверждение B было бы верно (хотя оно заведомо неверно). Полученное противоречие показывает, что исходное предположение было неверно (предположение, что А - ложно). А потому утверждение А - истинно по закону двойного отрицания (¬(¬А) равносильно А).
Пример:
Доказать, что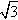 
- иррациональное число.
Доказательство: Докажем утверждение от обратного. Допустим число 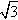- рациональное. Тогда по определению рационального числа, его можно представить в виде несократимой дроби m/n, где m ∈ Z, n ∈ N.
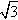= m/n. Поднесем в квадрат:
3 = m2/n2.
m2 = 3n2.
m2 делится на 3, а значит и m делится на 3. Тогда m2 делится на 9. Раз так, то и n2 делится на 3, а потому и n делится на 3. Получается - что дробь m/n сократима. Мы пришли к противоречию исходного суждения (что число рационально). Потому число 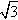- иррациональное.
2. Метод математической индукции.
Один из основных методов доказательства. Смысл его состоит в следующем. Допустим у нас есть последовательность утверждений A1, A2, ... , An, An+1, ..., где n ∈ N. Все утверждения будут истинными, если:
1) Будет доказана база индукции, т.е. истинность утверждения A1;
2) Будет доказан переход, т.е. для любого n будет доказано, что если утверждение An - верно, то верно и утверждение An+1.
Пример:
Доказать, что если k ∈ N, то число k2 - k - четное.
Решение: Решим задачу с помощью метода математической индукции.
Проверим базу индукции - при k = 1, k2 - k = 0 - число четное.
Докажем переход. Допустим при некотором k = n, число n2 - n - четное. Докажем, что k = n+1 число (n + 1)2 - (n + 1) - тоже четное. Но (n + 1)2 - (n + 1) = n2 + 2n + 1 - n - 1 = n2 + n = n2 - n + 2n. Число n2 - n - четное, согласно предположению и 2n - четное. Сумма четных чисел - четная. Переход доказан.
Потому при любом k ∈ N число k2 - k - четное.
Существуют и другие вариации метода математической индукции. Например, есть последовательность утверждений B1, B2, ... , Bn, Bn+1, ..., где n ∈ N. Все утверждения будут истинными, если:
1) Будет доказана истинность утверждения B1;
2) Для любого n будет доказано, что если утверждения B1, ... , Bn - верны, то верно и утверждение Bn+1.
Это т.н. принцип полной математической индукции.
3. Принцип Дирихле.
Очевидный, простой в понимании, но в то же время, довольно мощный метод решения задач состоит в следующем: если A элементов разбиты на a групп, причем A > a, то хотя в одной группе будет находится более одного элемента (A, a ∈ N). Данный принцип, являющийся одной из форм метода от противного, был сформулирован известным немецким математиком Дирихле и зачастую формулируется так: Если в n клетках сидит m зайцев и m > n, то хотя бы в одной клетке сидят более одного зайца.
Главная цель в решении такого рода задач - определение "зайцев" и "клеток" в даной конкретной задаче. Чаще всего - это самый трудный этап в решении, так как выбор не всегда очевиден.
Очень ценным является то, что даный метод дает неконструктивное доказательство (ведь мы точно не можем указать, в какой именно клетке находятся более одного зайца); в отличие от конструктивного, когда нужно идти путем полного построения или явно указывать искомый объект, что зачастую приводит к значительным трудностям и затратам времени.
Пример:
Дано 7 различных натуральных чисел. Доказать, что из них можно выбрать два числа, чтобы их разность делилась на 6.
Доказательство: При делении на 6 существует шесть различных остатков: 0, 1, 2, 3, 4, 5. Применим принцип Дирихле. В даному случае "клетками" будут остатки, а "зайцами" - числа. Зайцев 7, а чисел 6. Потому как минимум два числа имеют одинаковые остатки.
Пусть эти числа x и y (x, y ∈ N)
Тогда x = 6p + r, а y = 6q + r. А значит x - y = 6(p - q).
Что и требовалось доказать.
4. Метод раскраски..
Суть данного метода состоит в следующем. Раскрасив некоторые ключевые элементы, которые фигурируют в задаче в несколько цветов, исследовать, что будет происходить, если выполнять условия задачи. Цвет позволяет значительно упростить понимание процесса, фигурируемого в условии, и зачастую приводит к решению. Этот метод позволяет эффективно решать ряд задач, в частности, игровые и шахматные задачи.
Пример:
Дан квадрат клетчатой бумаги размером 8 x 8, из которого вырезаны две крайние диагональные клетки (верхняя-правая и нижняя-левая). Можно ли полученную фигуру покрыть прямоугольниками размером 1 x 2?
Решение: Раскрасим наш обрезанный квадрат с помощью двух цветов в шахматную расцветку. Заметим, что отрезанные диагональные клетки будут одного цвета. Отметим также, что в нашем раскрашенном квадрате любые соседние две клетки (имеющие общую сторону) будут разного цвета. Это значит, что любой прямоугольник размером 1 x 2, которым мы будем пытаться покрыть обрезанный квадрат будет покрывать клетки обоих цветов. И если мы сможем покрыть обрезанный квадрат прямоугольниками 1 x 2, то будет покрыто одинаковое количество клеток с разными цветами; то есть фигура должна содержать одинаковое количество клеток обоих цветов. Но так как мы отрезали диагональные клетки одного цвета, то их количество в обрезанном квадрате на две меньше. Это означает, что мы не сможем польностью покрыть указанный обрезанный квадрат прямоугольниками 1 x 2.
