Найти log₆9, если известно, что log₆2 = k.

___________________________________

Имеем, log₆9 = log₆3² = 2·log₆3 = 2·log₆⁶/₂ = 2(log₆6 - log₆2) = 2(1 - k).

Ответ: 2(1 - k).

Решить уравнение lg(x + 1.5) = -lgx.

______________________________

Имеем lg(x + 1.5) + lgx = 0. Если мы сделаем переход к уравнению lgx(x + 1.5) = 0, мы расширим область определения исходного уравнения. Однако следующая система равносильна исходному уравнению:

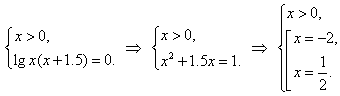
Откуда и получаем ответ: x = ½.

Ответ: x = ½.

Решить уравнение ^{log₂(9 - 2x)}/_{(3 - x)} = 1.
    __________________________________

Сразу укажем, что x ≠ 3 и проделаем следующие превращения:

log₂(9 - 2^x) = 3 - x; Далее используем определение логаримфа:

9 - 2^x = 2^{3 - x};

2^x + ⁸/_2^x - 9 = 0;

(2^x)² - 9·2^x + 8 = 0; Решения этого квадратного уравнения следующие:

2^x = 1 или 2^x = 8. Т.е. x = 0 или x = 3. Но так как решение x = 3 не попадает в ОДЗ исходного уравнения (мы записали это в самом начале), то ответ единственный: x = 0.

Ответ: x = 0.

Решить уравнение log₅(x - 2) + log_√5(x³ - 2) + log_0.2(x - 2) = 4.

__________________________________________________

Укажем, что x > 2 (ОДЗ). Далее, сводим все логаримфы к единому основанию 5:

log₅(x - 2) + 2·log₅(x³ - 2) - log₅(x - 2) = 4.

2·log₅(x³ - 2) = 4.

log₅(x³ - 2) = log₅25.

x³ - 2 = 25.

x³ = 27.

x = 3. Ответ подходит под ОДЗ.

Ответ: x = 3.