Упростить выражение a⁵a^-3a² / a³a^-4a^-1.

_________________________________

Пользуемся свойствами степеней.

В числителе получаем a⁵a^-3a² = a^5-3+2 = a⁴.

В знаменателе - a³a^-4a^-1 = a^3-4-1 = a^-2.

В итоге a⁴ / a^-2 = a⁶.

Ответ: a⁶

Упростить выражение z ^{(p - 3) / (p2 + 3p)} : z ^{12 / (9 - p2)} · z ^{3 / (3p - p2)} .

_________________________________________________

Пользуемся свойствами степеней и делаем преобразования:

z ^{(p - 3) / (p2 + 3p)} : z ^{12 / (9 - p2)} · z ^{3 / (3p - p2)} = z ^{(p - 3) / p · (p + 3) - 12 / (3 - p) · (3 + p) + 3 / p · (3 - p)} .

Далее упрощаем значение степени z. Сводим к общему знаменателю:

(p - 3) / [p(p + 3)] - 12 / [(3 - p)(3 + p)] + 3 / [p(3 - p)] =

[(p - 3)² + 12p - 3(p + 3)] / [p(p + 3)(p - 3)] = [p² - 6p + 9 + 12p - 3p - 9] / [p(p + 3)(p - 3)] =

[p² + 3p] / [(p² + 3p)(p - 3)] = 1/(p - 3)

Потому исходное выражение будет иметь вид z ^{1 / (p - 3)}

Ответ: z ^{1 / (p - 3)}

Упростить выражение .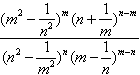

______________________________________

Пользуясь свойствами степеней и формулами сокращенного умножения делаем следующие преобразования:

= = =

= = .

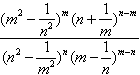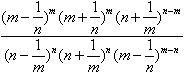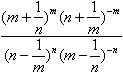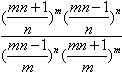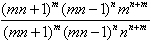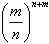Ответ: .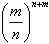

Упростить выражение √7 - 2√12.

____________________________

Чтобы упростить данное выражение попробуем выделить под корнем полный квадрат:

√7 - 2√12 = √7 - 4√3 = √4 - 4√3 + 3 = √(2 - √3)² = |2 - √3| = 2 - √3

Ответ: 2 - √3