На данный момент этот раздел содержит обобщенный материал по всему курсу стереометрии. Стереометрия - раздел геометрии, в котором изучаются фигуры в пространстве. В будущем этот материал будет разделен на несколько - по конкретной тематике.

Прямоугольный параллелепипед.

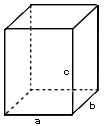
V_парал = abc.

Призма.

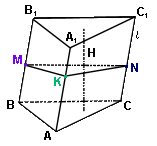
MKN - перпендикулярное (к ребру СС₁) сечение;

V_призм = SH, где S - площадь основания, H - высота призмы;

V_призм = S_⊥l, где S_⊥ - площадь перпендикулярного сечения MKN;

Площадь боковой поверхности призмы: S_{бок. призм} = P_⊥l, где P_⊥ - периметр перпендикулярного сечения MKN;

Пирамида.

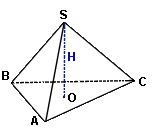
V_пирам = ¹/₃SH, где S - площадь основания, H - высота пирамиды;

Если пирамида правильная (т.е. в основании правильный многоугольник, а все боковые грани - равные равнобедренные треугольники), то площадь боковой поверхности равна:

S_{бок.пр.пирам} = ½ Ph, где P - периметр основания, h - высота боковой грани (апофема).

Усеченная пирамида.

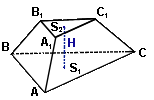
V_{ус.пирам} = ¹/₃H(S₁ + √S₁S₂ + S₂), где H - высота, S₁, S₂ - площади оснований усеченной пирамиды;

Если усеченная пирамида - правильная (т.е. сечение проводили с правильной пирамидой), то площадь боковой поверхности равна:

S_{бок.ус.пирам} = ½ (P₁ + P₂)h, где P₁, P₂ - периметры оснований, h - высота боковой грани (апофема).

Цилиндр.

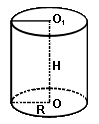
V_цил = πR²H, где R - радиус основания, H - высота цилиндра;

Площадь боковой поверхности цилиндра S_{бок.пов.цил} = 2πRH, где R - радиус основания, H - высота цилиндра.

Конус.

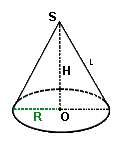
V_кон = ¹/₃πR²H, где R - радиус основания, H - высота конуса;

Площадь боковой поверхности конуса S_{бок.кон} = πRl, где R - радиус основания, l - образующая конуса.

Усеченный конус.

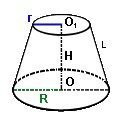
V_ус.кон = ¹/₃πH(R² + Rr + r²), где R, r - радиусы оснований, H - высота усеченного конуса;

Площадь боковой поверхности усеченного конуса S_{бок.ус.кон} = π(R + r)l, где R, r - радиусы оснований, l - образующая усеченного конуса.

Шар, сфера.

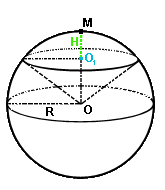
Объем шара V_шара = ⁴/₃πR³, где R - радиус шара;

Объем шарового сегмента V_{шар.сегм} = πH²(R - ¹/₃H), где H = MO₁ - высота шарового сегмента, R = MO - радиус шара;

Объем шарового сектора V_{шар.сект} = ²/₃πR²H, где H = MO₁ - высота сегментной части сектора, R = MO - радиус шара;

Площадь сферы S_сф = 4πR², где R - радиус сферы;

Площадь сферического сегмента S_{сф.сегм} = 2πRH, где R - радиус сферы, H = MO₁ - высота сегмента.