Определение
Рассмотрим окружность радиуса R с центром в точке O. Положительный угол AOK создан вращением радиус-вектора OA (|OA| = R) по направлению против часовой стрелки.
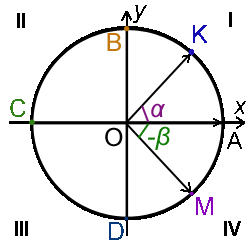
Угол 1° (1 градус) - это угол, который опирается на дугу, которая равна 1/360 части окружности. На рисунке выше угол ∠ AOK = α°, ∠ AOB = 90°, ∠ AOC = 180°, ∠ AOD = 270°, ∠ AOA = 360°. Вся окружность делится на 360°, один градус содержит в себе 60 минут (60'), одна минута содержит в себе 60 секунд (60").
Осями координат окружность делится на четыре четверти. Отрицательные углы откладываем от оси Ox в направлении движения часовой стрелки (на рисунке выше ∠ AOM = -β° - отрицательный угол).
Кроме градусного измерения угла используется измерения угла в радианах: 1 рад - это угол, который опирается на дугу, длина которой равна радиусу. Поскольку длина окружности равна 2πR, то угол 360° = 2π рад. Исходя из этого
1 рад = 360°/2π = 57°17'44",
1° = 2π/360° рад = π/180° рад.
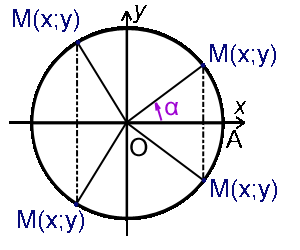
На окружности радиуса R выберем произвольную точку M(x; y), ∠ AOM = α, |OM| = R (см. рисунок выше). Определим тригонометрические функции угла α - синус (sin α), косинус (cos α), тангенс (tg α) и котангенс (ctg α):
sin α = y/R, cos α = x/R, tg α = y/x, ctg α = x/y.
Аналогично определяем тригонометрические функции произвольного угла (независимо от положения точки M она может находится в любой четверти I, II, III или IV).
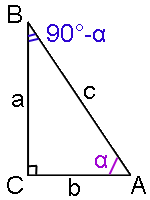
В прямоугольном треугольнике определим тригонометрически функции следующим образом:
sin α = a/c, cos α = b/c, tg α = a/b, ctg α = b/a,
где a - катет, лежащий напротив угла α, b - катет, прилегающий к углу α, c - гипотенуза.
Определим знаки тригонометрических функций у разных четвертях:
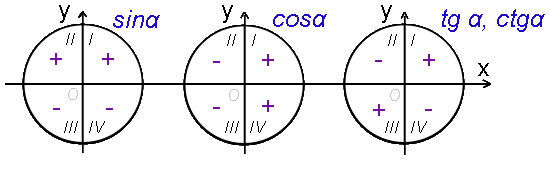
Связь между тригонометрическими функциями одного аргумента:
1. sin2 α + cos2 α = 1;
2. tg α · ctg α = 1;
3. 1 + tg2 α = 1/cos2 α; 1 + ctg2 α = 1/sin2 α;
4. sin (π/2 - α) = cos α; cos (π/2 - α) = sin α
Формулы суммы и разности.
1. cos (α + β) = cos α · cos β - sin α · sin β;
2. cos (α - β) = cos α · cos β + sin α · sin β;
3. sin (α + β) = sin α · cos β + cos α · sin β;
4. sin (α - β) = sin α · cos β - cos α · sin β;
5. tg (α + β) = (tg α + tg β)/(1 - tg α · tg β);
6. tg (α - β) = (tg α - tg β)/(1 + tg α · tg β).
Формулы для функций двойного, тройного углов.
1. sin 2α = 2 sin α · cos α = 2tg α/(1 + tg2 α);
2. cos 2α = cos2 α - sin2 α = 2cos2 α - 1 = (1 - tg2 α)/(1 + tg2 α);
3. tg 2α = 2tg α/(1 - tg2 α);
4. sin 3α = sin α (3 - 4sin2 α);
5. cos 3α = cos α (4 cos2 α - 3);
6. tg 3α = (3tg α - tg3 α)/(1 - 3tg2 α).
Формулы преобразования суммы и разности в произведение.
1. cos α + cos β = 2cos(α + β)/2 · cos(α - β)/2;
2. cos α - cos β = -2sin(α + β)/2 · sin(α - β)/2;
3. sin α + sin β = 2sin(α + β)/2 · cos(α - β)/2;
4. sin α - sin β = 2cos(α + β)/2 · sin(α - β)/2;
5. tg α + tg β = sin(α + β)/cos α · cos β;
6. tg α - tg β = sin(α - β)/cos α · cos β.
Формулы преобразования произведения в сумму.
1. cos α · cos β = ½ [cos(α - β) + cos(α + β)];
2. sin α · sin β = ½ [cos(α - β) - cos(α + β)];
3. sin α · cos β = ½ [sin(α + β) + sin(α - β)].